The professional’s guide to Quantum Technology
- Preface: Why this guide?
- Part 1 – The background: Why are we so enthusiastic about Quantum Technology?
- Part 2 – The applications: What problems will we solve with Quantum Computers?
- Part 3 – The developments: Searching for a killer application, with a closer look at artificial fertilizer
- Part 4 – The applications of Quantum Networks
- Part 5 – Timelines: When can we expect a useful quantum computer?
- Part 6 – Getting started: What steps should your organization take?
- Part 7 – The hardware: Why you should care about different qubits
- Part 8 – The threat: The impact on cybersecurity
- Part 9 – Scaling up: Why we need error correction
- Further reading: An overview of resources
Part 5 – Timelines:
When can we expect a useful Quantum Computer?
The billion-dollar question in our field is:
When will quantum computers outperform conventional computers on relevant problems?
Unfortunately, nobody really knows. We could give, say, 2036 as a reasonable estimate, and many people may clamp hope to such estimations. You may even jump straight to our conclusions. However, these numbers strongly rely on unpredictable breakthroughs, and past predictions regularly proved inaccurate. Moreover, a relevant quantum computer won’t just suddenly appear: there’s a continuous evolution where these devices will become increasingly capable. That’s why, in this chapter, we address how future predictions are made, and what will happen on the path towards large-scale quantum computation.
What parameters are relevant?
Compared to currently available technology, we’d require a fundamental improvement to these specifications:
- Number of qubits
- Accuracy of elementary operations (i.e.: ability to perform long computations without making mistakes). Sufficient accuracy likely requires error correction.
In the following, we may use the term quantum gate to mean one elementary operation on a quantum computer. You should compare these quantum gates to their classical counterparts, like NOT and OR that you may find in classical electronics.
There are quite a few other parameters that matter (such as the connectivity, the available set of gates, the speed of operations, and so forth). We choose to simplify matters by presenting a limited perspective with just the number of qubits and gate accuracies, which is sufficient a rough estimate.
The relevance of accuracy is often overlooked, perhaps because this hardly plays a role for classical computers (which operate perfectly for basically all intents and purposes). The problem is as follows: every gate we perform on the quantum computer has a small chance of introducing an error. The more steps a computation takes, the larger the chance that the computation fails. In other words: harder problems put more stringent requirements on the quantum computer’s hardware, and require more accurate operations.
Of course, our main focus is on massive-scale computational problems that take hours or even weeks on classical machines.
To illustrate, imagine a quantum computer where each elementary step (“gate”) has a 1:1000 chance to introduce an error. This computer may suffice for computations of merely 100 gates, but as soon as of the order of 1000 or more gates are needed, the probability that the computer’s output is incorrect becomes quite significant.
What if we need to run a circuit of 1 million gates? If the computer has sufficiently many qubits, we will use error correction to lower the probability of error to much less than one-in-a-million.
We often state the ‘error’ of a gate, rather than the ‘accuracy’. For example, a gate with 1% chance of error can be said to have 99% ‘accuracy’. Scientists like to define these numbers more precise by talking about gate fidelities or coherence times.
Luckily, there is a well-established field of quantum error correction. It allows us to combine many ‘physical qubits’ available on the device (think of the order of 1000) into a single, more accurate ‘logical qubit’, on which gates have a smaller chance of error (say, by a factor 1 billion). This allows much longer computations. Error correction allows a trade-off between the number of available qubits and gate accuracy.
For more details, see the chapter on error correction.
In this chapter, we simplify the predictions down to only the number of physical qubits, so that we have a single parameter to study. This means that, for longer computations (or better accuracies), we accounts for additional qubits to achieve the necessary gate accuracies.
Back to the main question: When can we expect a large quantum computer?
For now, let’s keep things relatively simple, and break our billion-dollar question into two parts:
- How many qubits do we need for relevant applications?
- How long will it take before we have that many qubits?
How many qubits are needed?
In Part 2, we discussed the three main applications of quantum computers: quantum simulation, breaking cryptography, and optimization.
The most concrete numbers can be given for Shor’s algorithm (breaking cryptography), where we have a very clear problem to tackle: obtain a private (secret) key from a widely-used cryptosystem, like the RSA-2048 protocol. This is the perfect benchmark because there can be no discussion about whether the problem is solved: one either obtains the correct key, or one doesn’t. Moreover, for this benchmark, we’re quite convinced that even the best classical computers can’t solve the problem (or else we you shouldn’t use internet banking or trust software updates).
A recent estimate finds that a plausible quantum computer would require roughly 20 million ‘reasonably good’ physical qubits to factor a 2048-bit number. The whole computation would take about 8 hours. Such estimates require several assumptions on what a quantum computer would look like in the future. In this case, the authors assume qubits are built using superconducting circuits, which are laid out in a square grid. Error correction is assumed to be done using the so-called surface code, assuming the best-known methods for error correction in 2020. Note that future breakthroughs could reduce the required time and number of qubits even further.
For chemistry and material simulation, it’s a lot harder to give estimates, because there is not just a single problem to tackle here: one typically uses computers to gradually improve our understanding of a complex structure or chemical reaction. This should be combined with theoretical reasoning and practical experiments. Moreover, classical computers are often able to perform the same computations that the quantum computer would make, at the cost of making certain assumptions or simplifications. There’s a fuzzy region between ‘classically tractable’ and ‘quantum advantage’.
One way to define a concrete task is to ask for the energetic cost of certain molecular configurations. The benchmark here is to provide energies more accurately than done in conventional experiments: one canonically takes the ‘chemical accuracy’ of roughly 1 kcal/mol as the precision to beat. Then, of course, we should focus on molecules where classical computers cannot already achieve such accuracies.
Note that the accuracy of a chemical energy should not be confused with the accuracy of a quantum gate, which is a whole different number.
A highly promising and well-studied benchmark problem is the simulation of the so-called FeMo cofactor, in short: FeMoco. This molecule is relevant when bacteria produce Ammonia (NH3), a compound that is of great relevance to a plant’s root system. A better understanding of this process could help us reduce the ridiculously large carbon emissions now associated with the production of artificial fertilizer. We give more details in a separate chapter.
Simulation of FeMoco is believed to require around 4 million qubits (and around 4 days of computation for a single simulation run). Assumptions of the hardware and error correction are similar to the case of Shor’s algorithm: the estimate is based on a square grid of superconducting qubits, using surface code as the method to correct errors.
For a different enzyme, namely cytochrome P450, it has been estimated that around 5 million qubits are needed (again taking roughly 4 days of computation). Altogether, we conclude that a couple million qubits (of sufficiently high quality) may make quantum computers relevant for R&D in chemistry.
Further reading:
- A case study of FeMoco as a killer application for quantum computers
- University of Leiden’s research page on why simulating FeMoCo is the Killer Application for quantum computers.
For many optimization problems, it’s practically impossible to give reasonable estimates. For one, a true killer algorithm for optimization problems is not known yet. The algorithms that are presented as the most promising are often heuristic, meaning that scientists do not know how long an algorithm will take to find solutions. This can happen, for example, when an algorithm repeats a certain loop until a stopping criterion has been met.
This may come as a shock, considering the many news items that report how quantum computers may already solve practical problems. But don’t be fooled: these articles state that quantum computers can indeed solve relatively simple problems, but often fail to mention that there exist different approaches by which classical computers can solve the same problems much, much faster.
Many optimization problems have a plethora of potential solutions, but the goal is to find the optimal solution (say, the one that incurs the least costs or gets you to your destination the fastest). The solution space is often so large that we don’t even know if we hit the optimal solution, but we’re okay with finding one that’s pretty close. Several papers claim that a quantum computer already finds solutions faster, but in all cases, worrying sacrifices were made for the optimality of the solutions.
One of the leading sources of wild claims is D-Wave’s quantum annealer. This is a ‘limited’ quantum computer that cannot run every quantum algorithm, but it’s extremely good a one specific algorithm, called “quantum annealing”. With around 5000 qubits, it can handle reasonably large problems, and several companies have tried their hands at this machine. The results obtained through today’s quantum annealing approaches are likely much more easily achieved by putting a similar amount of effort into a good classical solution.
| Application | How well can we estimate qubit requirements? | Use case example | Qubits needed? | Gate error assumed? |
|---|---|---|---|---|
| Breaking cryptography | Good | Cracking RSA-2048 | ~ 20 million | ~ 0.1% |
| Chemistry | Reasonable | Simulation of FeMoco | ~ 4 million | ~ 0.1% |
| Optimization / AI | Bad | ? | ? |
What about NISQ machines?
Current quantum computers are somewhat small and not yet capable of large-scale error correction: they are Noisy Intermediate Scale Quantum (NISQ) devices. Several parties claim that these devices may already perform useful computations without error correction. So far, we have not seen convincing evidence, but it is certainly possible that future breakthroughs make this possible. If so, quantum computers would become useful even sooner than we predict here.
Further reading: Professor Sankar Das Sarma on the lack of convincing NISQ applications.
How long until we have million-qubit machines?
We highlight a few sources that we can use to predict technological developments:
- Road maps and claims of hardware manufacturers
- Surveys to experts
- Extrapolation of Moore’s law
What do manufacturers say?
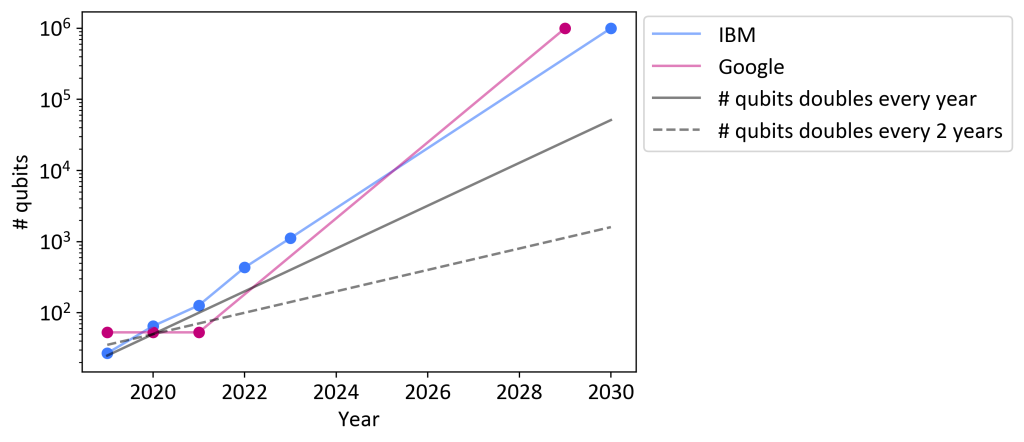
IBM has the most explicit road map. As of 2022, they predict to have over 1000 qubits by 2023, and 1 million qubits in 2030. Google even thinks of building a 1M qubit device by 2029. Unfortunately, such claims often cannot be found on the manufacturer’s websites, but are taken by journalists from talks and presentations. Both Google and IBM work on superconducting qubits.
Similarly, a start-up called PsiQuantum is reported to work towards a million photonic qubits by 2025, which seems somewhat unlikely because the company has not publicly demonstrated any successes so far.
IonQ displays its road map in a different format: they aim to have 1024 algorithmic qubits by 2028. This means that IonQ will have at least this number of qubits, but also guarantees sufficient gate accuracy to be able to run reasonably long circuits. It’s unclear whether a simple form of error correction may be needed to achieve this. If so, the actual number of physical qubits may be some orders of magnitude higher. Quantinuum (previously Honeywell Quantum Solutions) makes less concrete predictions, but expects fault-tolerant computing by 2030 (meaning that significant error correction is in place). In terms of today’s hardware, Quantinuum holds a record with roughly 19 algorithmic qubits.
In the figure below, we plot the road maps of Google and IBM, and compare these to Moore’s law.
What does Moore’s law say?
One could assume that quantum computers will ‘grow’ at a similar rate as classical computers. Moore’s law states that the number of transistors in a dense integrated circuit grows exponentially: the number doubles roughly every two years. This has been a surprisingly accurate predictor for the development of classical IT. If we apply Moore’s law to quantum, to get from 100 to 1M qubits would require 28.5 years – predicting that the 1M mark won’t be passed until 2048. Clearly, most hardware manufacturers are more optimistic. If we assume the number of qubits doubles each year, one would predict that 1M-qubit machines will be available around 2035. While doubling a quantum computer’s size each year is already a daunting challenge, IBM and Google set the bar even higher for themselves, hoping to double every 7-9 months.
What do experts say?
The Global Risk Institute conducts yearly surveys, asking experts to state the likelihood that quantum computers pose a significant threat to public-key cryptography 5 years from now. Similarly, respondents would also estimate the likeliness 10, 15, 20, and 30 years away.
This essentially boils down to the question: when will a quantum computer be built that can run Shor’s algorithm to crack RSA-2048? We previously saw that around 20 million qubits would be needed for this.
The results from December 2023, gathered from 37 quantum experts from academia and industry, are displayed below.
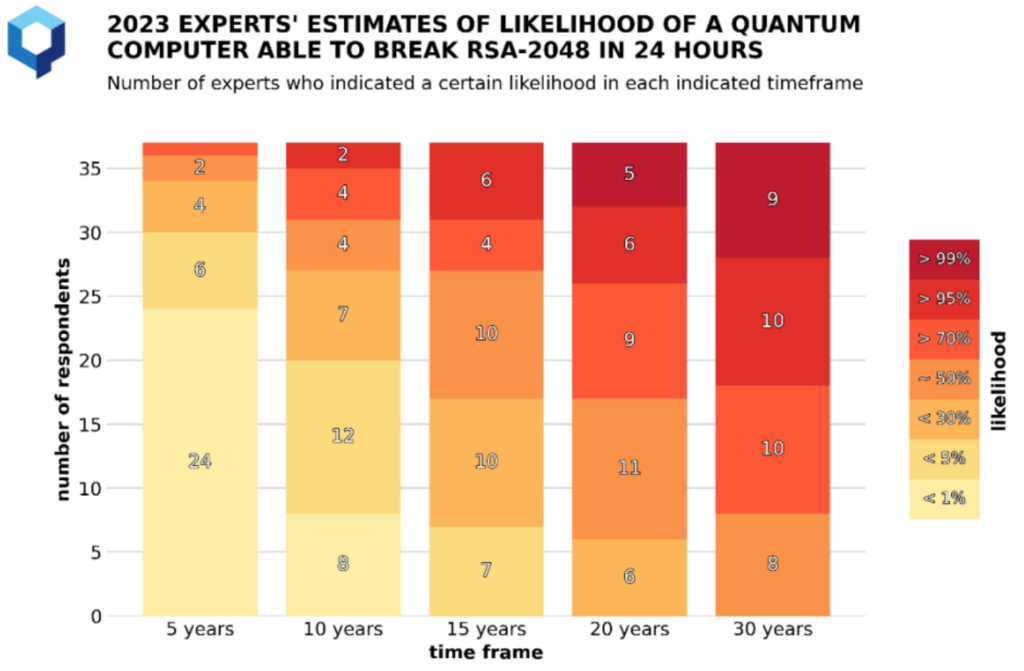
Let’s look at the column labeled ‘5 years’. A total of 24 correspondents indicate that there is less than 1% chance that quantum computers pose a security threat in the next five years. A single person is quite pessimistic and assigns >70% chance that this will happen. On average, experts say that there’s a fairly small chance that quantum computers will pose a threat to cryptography in the next 5 years.
Further to the right, the ratios shift: looking at 20 years from now, the majority of experts believe that quantum computers pose a serious threat: over half of them assign a likelihood of 70% or more.
It appears that the majority of experts believe that the tipping point is between 10-20 years from now. We could pick 3036 (15 years from now) as a point where experts assign, on average, a roughly 50% chance to see a quantum computer capable of running Shor’s algorithm. However, we should take into account a significant uncertainty: several experts make wildly varying estimates, and there’s no clear conclusion about the quantum computer’s impact in the next 30 years.
These experts are likely aware of hardware manufacturer’s road maps and make predictions that seem well in line with IBM’s vision on hardware, as we shall see below.
Conclusion: when will a quantum computer solve relevant problems?
In the figure below, we extrapolate IBM’s road map, assuming the same doubling time of roughly every eight-and-a-half months. We also indicate the predictions of Moore’s law with a doubling time of 1 or 2 years.
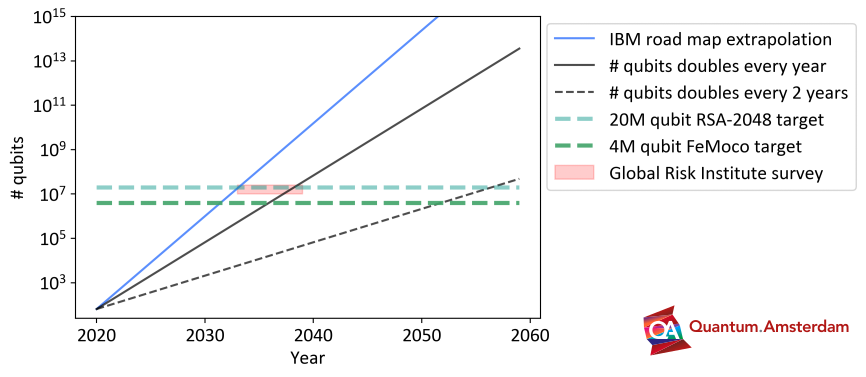
If IBM manages to adhere to its road map, relevant applications like cracking RSA and simulating FeMoco should be possible in the early 2030s. This holds, provided that gate accuracies and error correction are also evolving at a commensurate pace.
However, the exponential nature of qubit growth makes timeline predictions strongly dependent on the doubling time. If we assume regular Moore’s law (with a doubling time of 2 years), one shouldn’t expect 4 million qubits before the 2050s.
The ‘majority’ expert prediction according to the Global Risk Institute is separately indicated in the region around around 2033-2039 (light red area). It sits largely in between the pace of IBM and the yearly doubling version of Moore’s law.
Final words
Our analysis has its limitations: we considered just two use-cases of a quantum computer (which happen to be well-studied), but it is not unlikely that new, shorter-term applications will be found.
Nevertheless, we believe that the above data gives a fairly accurate outlook of future developments. Optimists may follow manufacturer’s roadmaps, pessimists will point at the 2-year doubling time of Moore’s law, and the truth is likely somewhere in between: we consider somewhere in the 2030s or early 2040s seems a reasonable estimate for relevant large-scale quantum computers. We stress that such estimates assume that there is not just a race for the largest numbers of qubits, but that gate accuracies and error correction implementations should evolve along at a similar pace.